Introduction

In this post, I'd like to record my experience of studying TFlearn.

Ingredient

To build a functional network, we should know how a convolutional layer is created and initialized. For layers in convolutional network, there are three kinds which are input layer, hidden layer and output layer. I will first show you what a layer looks like, and then explain all the parameters to you.

Input layer

Input layer is created and initialized by TFlearn built-in function input_data and the code is:

network = input_data(shape=[None, input_size, 1], name='input')

From above, I create an input layer with the size None*input_size*1. None means no restriction to the first dimension of the input tensor and this is for sequential decision when you cannot anticipate how many input data you will receive. As we know, input data is also called a tensor, and tensor is the extension of matrix which means it may contain uncertain dimension such as 1-d, 2-d, 3-d, ... so the input layer is initialized as a tensor and all following connected layers try to change the initial tensor to another shape. Input_size is an input parameter and it can be any number. 1 is size of the third dimension. So what I create is a 3-d tensor named input and although size the third dimension is 1, it still differs from a matrix because the third dimension is not a scalar but a 1-d tensor (or you can call it an array).

Source code of input_data is:

def input_data(shape=None, placeholder=None, dtype=tf.float32,
               data_preprocessing=None, data_augmentation=None,
               name="InputData"):
    """ Input Data.
  
    Input:
        List of `int` (Shape), to create a new placeholder.
            Or
        `Tensor` (Placeholder), to use an existing placeholder.
    Output:
        Placeholder Tensor with given shape.
    """ 

Hidden layer

Hidden layers are varies, because it is the essence of convolutional network. In this section, I will introduce three hidden layers, fully_connected, dropout and regression.

Fully-connected layer

network = fully_connected(network, 128, activation='relu')

Fully-connected layer use the former layer as input, and with no regard to the shape of former layer, it changes the tensor to a different size.

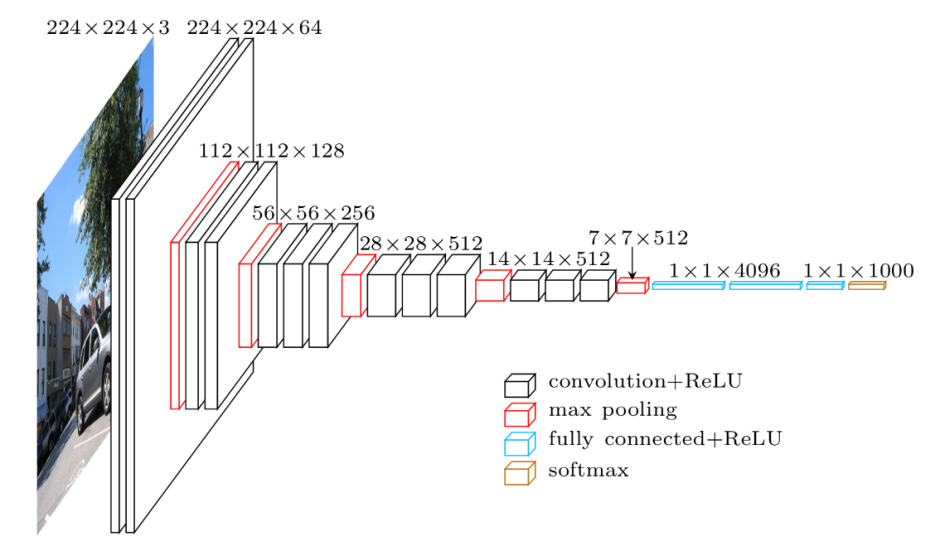
Let me explain why this built-in function fully_connected only has one size parameter 128. Frequently, the input has three dimensions (the image has three dimensions because it has width, height and three color channel RGB) and the convolutional kernel slip in dimension width and height like a slide window.

So when the layer in middle is not fully connected, the kernel use stride to make the image smaller while the number of kernel deepens it as shown in Figure VGG16 architecture.

Fully connected means the kernel has the same shape with the front layer (or image) and each number in the kernel is a one-on-one weight to front image. The parameter 128 means there are 128 kernels in the fully connected layer.

Tips

What's the difference between the four line below?

network = input_data(shape=[None, input_size, 1], name='input')
network = fully_connected(network, 128, activation='relu')

network = input_data(shape=[None, input_size], name='input')
network = fully_connected(network, 128, activation='relu')

In fact, there is not much difference between the 2 lines above and 2 lines below besides that the 2 lines below contain a series of scalars while the 2 lines above contain a series of arrays.

Dropout layer

network = dropout(network, 0.8)

Dropout layer is a magic layer which lets the network automatically miss some node to prevent over-fitting.

Regression layer

network = regression(network, optimizer='adam', learning_rate=LR, loss='categorical_crossentropy', name='targets')

The...

DNN layer

model = tflearn.DNN(network, tensorboard_dir='log')

The DNN layer is actually not defined in convolutional network architecture, and it is a wrapper or container which wrap the network. You can use the model where network is wrapped to estimate or predict.